Analiza statystyczna
Po opracowaniu przewodników zestawiono w tabeli ilości cmentarzy i ilości grobów w 6 przewodnikach, w kolumnach podane są liczby grobów na kolejnych cmentarzach dla poszczególnych lokalizacji, liczba wierszy jest równa liczbie cmentarzy.
Kielce
Łódź
Płock
Trójmiasto
Warszawa
Zielona Góra
2
1
1
1
1
1
6
1
2
1
1
5
8
1
3
1
1
23
9
1
6
1
1
17
1
9
1
2
2
2
2
2
2
2
2
3
2
3
6
2
3
8
3
8
9
3
16
9
3
15
3
4
4
10
11
12
Przygotowane dane były podstawą analizy statystycznej ilości cmentarzy i ilości grobów w 6 przewodnikach.
- Histogram liczby cmentarzy
Na podstawie powyższej tabeli opracowano drugą tabelę, w jej kolumnach podane są liczby cmentarzy z liczbami uwzględnionych grobów dla poszczególnych lokalizacji, a w wierszach liczby cmentarzy w poszczególnych lokalizacjach z możliwymi liczbami grobów.
Liczba grobów
Kielce
Łódź
Płock
Trójmiasto
Warszawa
Zielona Góra
Cmentarze
Groby
1
5
1
5
4
1
16
16
2
1
3
1
2
5
12
24
3
2
1
1
4
8
24
4
2
2
8
5
1
1
5
6
1
1
1
3
18
8
1
1
1
3
24
9
1
1
2
4
36
10
1
1
10
11
1
1
11
12
1
12
15
1
1
15
16
1
1
16
17
1
1
17
23
1
1
23
Cmentarze
5
12
5
13
18
3
56
Groby
42
33
21
59
67
29
259
Na podstawie tej tabeli został sporządzony histogram.
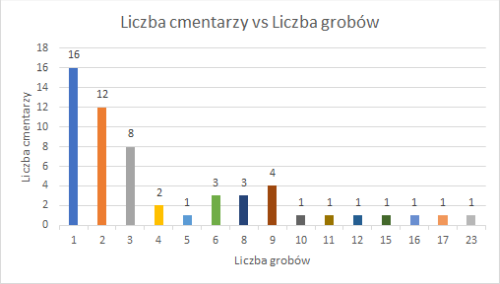
- Parametry rozkładu ilości grobów
Parametry rozkładu
Łącznie
Suma
42
41
21
59
67
29
259
Minimum
2
1
1
1
1
1
1
Maksimum
17
16
9
15
12
23
23
Średnia
8,4
3,41
4,2
4,54
3,72
9,67
4,62
Mediana
8
2
3
2
2,5
5
2,5
Moda
1
1
2
1
Odchylenie standardowe
5,5
4,42
3,27
4,48
3,49
11,72
4,83
Skośność
0,9
2,54
0,85
1,21
1,69
1,51
1,83
Wyniki dotyczące poszczególnych lokalizacji otrzymano przy pomocy narzędzia "Statystyki opisowe" pakietu Analysis ToolPak arkusza Excel na podstawie tablicy z danymi. Wyniki dotyczące wszystkich cmentarzy otrzymano przy pomocy tego samego narzędzia na podstawie połączonych kolumn w/w tablicy.
Wykresy sprządzono arkuszem Excel na podstawie pierwszego wiersza tabeli będącej podstawą histogramu oraz wybranych wierszy tabeli z parametrami rozkładu ilości grobów.
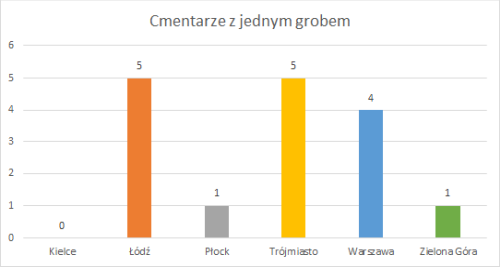
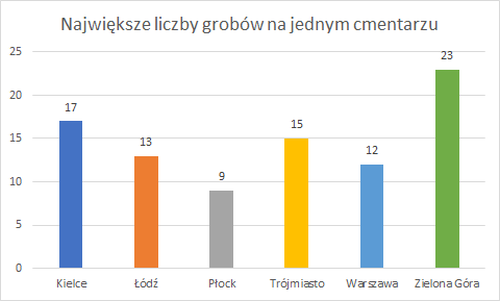
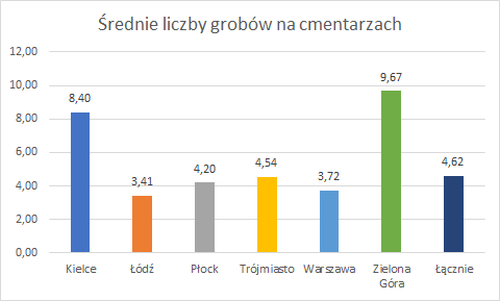
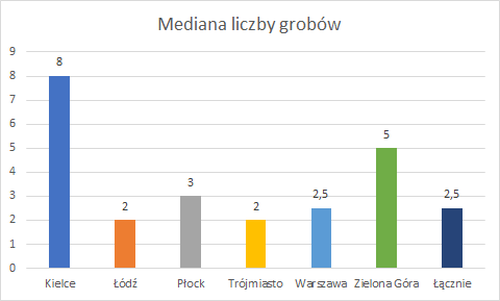
- Porównywanie rozkładów liczby grobów na cmentarzach
W punkcie poprzednim zostały obliczone parametry rozkładu. Kolejnym krokiem analizy mogło być na przykład weryfikacja hipotezy o równości wartości oczekiwanych liczby grobów, ale możliwe do wykorzystania testy wymagają między innymi normalności rozkładu, co nie jest spełnione.
Możliwe jest jednak sprawdzenie czy te rozkłady są takie same. W tym celu można wykorzystać test Kruskala-Wallisa oparty o rangi, porównuje on średnie wartości rang a nie średnie.
Hipotezą zerową jest równość dystrybuant rozkładów.
Średnie wartości rang przedstawiono na poniższym wykresie.

Na ich podstawie można obliczyć krytyczny poziom istotności, który jest w tym przypadku równy 0.3362
Oznacza to w szczególności, że na poziomie istotności < 0.05 nie istnieje istotna różnica pomiędzy rozkładami ilości grobów na cmentarzach w lokalizacjach obejmowanych przewodnikami.
Obliczenia wykonano kalkulatorem testu Kruskala-Wallisa w oparciu o dane przedstawione w tabeli z danymi.
- Współczynnik korelacji Pearsona pomiędzy liczbami cmentarzy i liczbami grobów w poszczególnych lokalizacjach.
r = 0,82
Obliczenie wykonano funkcją statystyczną "Współczynnik korelacji" arkusza Excel na podstawie dwóch ostatnich kolumn tabeli z danymi.
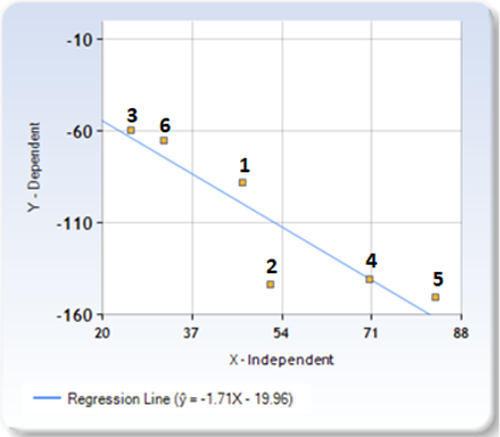
- Równanie regrsji liniowej pomiędzy liczbami grobów i liczbami cmentarzy w poszczególnych lokalizacjach
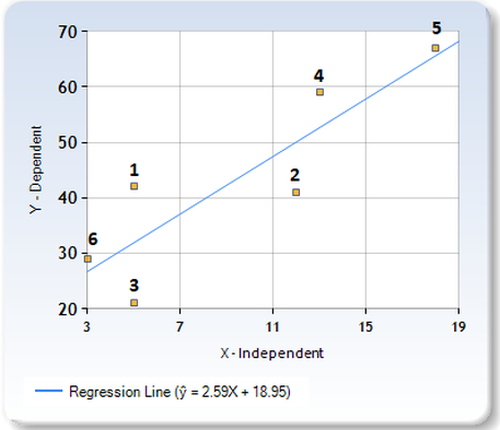
X - liczba cmentarzy (Independent)
ŷ - liczba grobów (Dependent)
1 - Kielce
2 - Łódź
3 - Płock
4 - Trójmiasto
5 - Warszawa
6 - Zielona Góra
Obliczenia wykonano kalkulatorem statystycznym na podstawie dwóch ostatnich kolumn tabeli z danymi.
- Analiza skupień
Na kilku cmentarzach jest duża liczba grobów, ich odwiedzenie podczas jednej wizyty nie jest praktycznie możliwe. Można je oczywiście wybrać zapoznając się z życiorysami. Innym sposobem jest wybranie w oparciu o datę urodzenia i datę śmierci, można tego dokonć wykonując analizę skupień.
W tej analizie zadana liczba elementów, których wzajemne zróżnicowanie określa np. odległośc euklidesowa, zostanie zaklasyfikowana do określonej liczby podzbiorów (skupień), zawierających obiekty „podobne”.
Poniżej przedstawiono wyniki tej analizy dla 23 grobów położonych na cmentarzu Komunalnym Starym w Zielonej Górze.
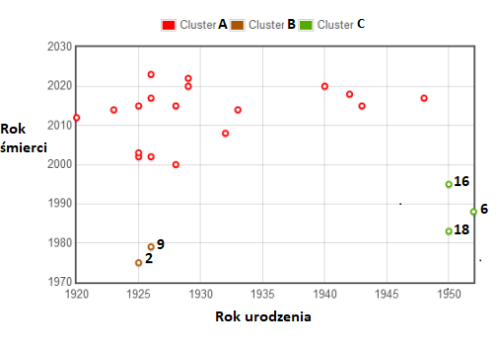
Groby zostały podzielone na 3 skupienia o licznościach: 18, 2 i 3.
Środki skupień
A 1930.4 2013.2
B 1925.5 1977.0
C 1950.7 1988.7
Elementy skupienia B
2 1925,1975 Grób Tadeusza Bedusa
9 1926,1979 Grób Benedykta Piekarskiego
Elementy skupienia C
6 1952,1988 Grób Andrzeja Lewandowskiego
16 1950,1995 Grób Zbigniewa Szelucha
18 1950,1983 Grób Andrzej Zembatego
Pozostałe groby należą do skupienia A.
Obliczenia wykonano przy pomocy kalkulatora statystycznego na podstawie przygotowanych danych w postaci roku urodzenia i roku śmierci kolejnych osób ujętych w przewodniku.
- Ocena zależności pomiędzy składowymi przewodników
Na zakończenie zbadano związek między dwoma zbiorami zmiennych:
- X1 Liczba cmentarzy
- X2 Liczba grobów
oraz
- Y1 Liczba pytań dot. pochowanych
- Y2 Liczba haseł w krzyżówkach dot. pochowanych
- Y3 Liczba pytań/haseł w testach/krzyżówkach dot. chorągwi
Wykorzystano do tego metodę korelacji kanonicznej.
Otrzymano, że zmienne kanoniczne są określone wzorami
U = 0,845*X1 + X2
V = 0,895*Y1 - 2,016*Y2 + Y3
Po obliczeniu ich wartości
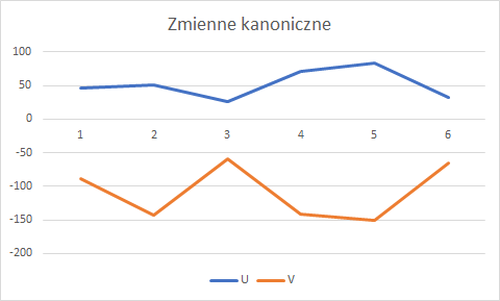
gdzie:
1 - Kielce
2 - Łódź
3 - Płock
4 - Trójmiasto
5 - Warszawa
6 - Zielona Góra
wyznaczono współczynnik korelacji
r = - 0,90
oraz równanie regresji
gdzie:
1 - Kielce
2 - Łódź
3 - Płock
4 - Trójmiasto
5 - Warszawa
6 - Zielona Góra
Obliczenia wykonano przy pomocy kalkulatorów internetowych i arkusza Excel na podstawie danych - przebieg obliczeń.
Kielce |
Łódź |
Płock |
Trójmiasto |
Warszawa |
Zielona Góra |
2 |
1 |
1 |
1 |
1 |
1 |
6 |
1 |
2 |
1 |
1 |
5 |
8 |
1 |
3 |
1 |
1 |
23 |
9 |
1 |
6 |
1 |
1 |
|
17 |
1 |
9 |
1 |
2 |
|
| 2 | 2 |
2 |
|||
2 |
2 |
2 |
|||
2 |
3 |
2 |
|||
3 |
6 |
2 |
|||
3 |
8 |
3 |
|||
8 |
9 |
3 |
|||
16 |
9 |
3 |
|||
15 |
3 |
||||
4 |
|||||
4 |
|||||
10 |
|||||
11 |
|||||
12 |
Na podstawie powyższej tabeli opracowano drugą tabelę, w jej kolumnach podane są liczby cmentarzy z liczbami uwzględnionych grobów dla poszczególnych lokalizacji, a w wierszach liczby cmentarzy w poszczególnych lokalizacjach z możliwymi liczbami grobów.
|
Liczba grobów |
Kielce |
Łódź |
Płock |
Trójmiasto |
Warszawa |
Zielona Góra |
Cmentarze |
Groby |
1 |
5 |
1 |
5 |
4 |
1 |
16 |
16 |
|
2 |
1 |
3 |
1 |
2 |
5 |
12 |
24 |
|
3 |
2 |
1 |
1 |
4 |
8 |
24 |
||
4 |
2 | 2 |
8 |
|||||
5 |
1 |
1 |
5 |
|||||
6 |
1 |
1 |
1 |
3 |
18 |
|||
8 |
1 |
1 |
1 |
3 |
24 |
|||
9 |
1 |
1 |
2 |
4 |
36 |
|||
10 |
1 |
1 |
10 |
|||||
11 |
1 |
1 |
11 |
|||||
12 |
1 |
12 |
||||||
15 |
1 |
1 |
15 |
|||||
16 |
1 |
1 |
16 |
|||||
17 |
1 |
1 |
17 |
|||||
23 |
1 |
1 |
23 |
|||||
Cmentarze |
5 |
12 |
5 |
13 |
18 |
3 |
56 |
|
Groby |
42 |
33 |
21 |
59 |
67 |
29 |
259 |
Na podstawie tej tabeli został sporządzony histogram.

|
Parametry rozkładu |
Łącznie |
||||||
|
Suma |
42 |
41 |
21 |
59 |
67 |
29 |
259 |
|
Minimum |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Maksimum |
17 |
16 |
9 |
15 |
12 |
23 |
23 |
|
Średnia |
8,4 |
3,41 |
4,2 |
4,54 |
3,72 |
9,67 |
4,62 |
|
Mediana |
8 |
2 |
3 |
2 |
2,5 |
5 |
2,5 |
|
Moda |
1 |
1 |
2 |
1 |
|||
|
Odchylenie standardowe |
5,5 |
4,42 |
3,27 |
4,48 |
3,49 |
11,72 |
4,83 |
|
Skośność |
0,9 |
2,54 |
0,85 |
1,21 |
1,69 |
1,51 |
1,83 |
Wyniki dotyczące poszczególnych lokalizacji otrzymano przy pomocy narzędzia "Statystyki opisowe" pakietu Analysis ToolPak arkusza Excel na podstawie tablicy z danymi. Wyniki dotyczące wszystkich cmentarzy otrzymano przy pomocy tego samego narzędzia na podstawie połączonych kolumn w/w tablicy.
Wykresy sprządzono arkuszem Excel na podstawie pierwszego wiersza tabeli będącej podstawą histogramu oraz wybranych wierszy tabeli z parametrami rozkładu ilości grobów.




W punkcie poprzednim zostały obliczone parametry rozkładu. Kolejnym krokiem analizy mogło być na przykład weryfikacja hipotezy o równości wartości oczekiwanych liczby grobów, ale możliwe do wykorzystania testy wymagają między innymi normalności rozkładu, co nie jest spełnione.
Możliwe jest jednak sprawdzenie czy te rozkłady są takie same. W tym celu można wykorzystać test Kruskala-Wallisa oparty o rangi, porównuje on średnie wartości rang a nie średnie.
Hipotezą zerową jest równość dystrybuant rozkładów.
Średnie wartości rang przedstawiono na poniższym wykresie.

Na ich podstawie można obliczyć krytyczny poziom istotności, który jest w tym przypadku równy 0.3362
Oznacza to w szczególności, że na poziomie istotności < 0.05 nie istnieje istotna różnica pomiędzy rozkładami ilości grobów na cmentarzach w lokalizacjach obejmowanych przewodnikami.
Obliczenia wykonano kalkulatorem testu Kruskala-Wallisa w oparciu o dane przedstawione w tabeli z danymi.
Obliczenie wykonano funkcją statystyczną "Współczynnik korelacji" arkusza Excel na podstawie dwóch ostatnich kolumn tabeli z danymi.

X - liczba cmentarzy (Independent)
ŷ - liczba grobów (Dependent)
1 - Kielce
2 - Łódź
3 - Płock
4 - Trójmiasto
5 - Warszawa
6 - Zielona Góra
Obliczenia wykonano kalkulatorem statystycznym na podstawie dwóch ostatnich kolumn tabeli z danymi.
Na kilku cmentarzach jest duża liczba grobów, ich odwiedzenie podczas jednej wizyty nie jest praktycznie możliwe. Można je oczywiście wybrać zapoznając się z życiorysami. Innym sposobem jest wybranie w oparciu o datę urodzenia i datę śmierci, można tego dokonć wykonując analizę skupień.
W tej analizie zadana liczba elementów, których wzajemne zróżnicowanie określa np. odległośc euklidesowa, zostanie zaklasyfikowana do określonej liczby podzbiorów (skupień), zawierających obiekty „podobne”.
Poniżej przedstawiono wyniki tej analizy dla 23 grobów położonych na cmentarzu Komunalnym Starym w Zielonej Górze.

Groby zostały podzielone na 3 skupienia o licznościach: 18, 2 i 3.
Środki skupień
A 1930.4 2013.2
B 1925.5 1977.0
C 1950.7 1988.7
Elementy skupienia B
2 1925,1975 Grób Tadeusza Bedusa
9 1926,1979 Grób Benedykta Piekarskiego
Elementy skupienia C
6 1952,1988 Grób Andrzeja Lewandowskiego
16 1950,1995 Grób Zbigniewa Szelucha
18 1950,1983 Grób Andrzej Zembatego
Pozostałe groby należą do skupienia A.
Obliczenia wykonano przy pomocy kalkulatora statystycznego na podstawie przygotowanych danych w postaci roku urodzenia i roku śmierci kolejnych osób ujętych w przewodniku.
Na zakończenie zbadano związek między dwoma zbiorami zmiennych:
- X1 Liczba cmentarzy
- X2 Liczba grobów
- Y1 Liczba pytań dot. pochowanych
- Y2 Liczba haseł w krzyżówkach dot. pochowanych
- Y3 Liczba pytań/haseł w testach/krzyżówkach dot. chorągwi
Wykorzystano do tego metodę korelacji kanonicznej.
Otrzymano, że zmienne kanoniczne są określone wzorami
V = 0,895*Y1 - 2,016*Y2 + Y3
Po obliczeniu ich wartości

gdzie:
1 - Kielce
2 - Łódź
3 - Płock
4 - Trójmiasto
5 - Warszawa
6 - Zielona Góra
wyznaczono współczynnik korelacji
oraz równanie regresji

gdzie:
1 - Kielce
2 - Łódź
3 - Płock
4 - Trójmiasto
5 - Warszawa
6 - Zielona Góra
Obliczenia wykonano przy pomocy kalkulatorów internetowych i arkusza Excel na podstawie danych - przebieg obliczeń.